
高考专题二次函数-精品之高中数学(理)黄金100题--- 精校解析Word版
27页1、第14题二次函数I题源探究黄金母题【例1】已知函数=,=()(1) 求,的单调区间;(2) 求,的最小值【解析】(1)由题知,=,=,当1时,0,当1时,0,当时,0,的单调减区间为,单调增区间为(1,+);的单调增区间为2,4(2)由(1)知,当时,=-1;当=2时,=0精彩解读【试题来源】人教版A版必修1第39页B组第1题【母题评析】本题主要考查利用二次函数的象研究二次函数的单调性和最值高考中的许多最值问题最值都可以转化为二次函数在某个区间上的最值问题,故本题是一个典型的二次函数问题【思路方法】二次函数问题,常常借助其象研究函数的单调性、对称性、在某个区间上的值域,借助象解对应的一元二次不等式和根的分布问题II考场精彩真题回放【例1】【2017高考山东理10】已知当时,函数的象与的象有且只有一个交点,则正实数的取值范围是ABC D【答案】B【解析】当时,单调递减,且,单调递增,且,此时有且仅有一个交点;当时,在上单调递增,要有且仅有一个交点,需,故选B【例2】【2017浙江卷】若函数f(x)=x2+ ax+b在区间0,1上的最大值是M,最小值是m,则M m()A与a有关,且与b有关
2、B与a有关,但与b无关C与a无关,且与b无关D与a无关,但与b有关【答案】B【解析】因为最值在中取,最值之差一定与无关,选B【例3】【2016高考新课标II】已知函数f(x)(xR)满足f(x)=f(2-x),若函数y=|x2-2x-3| 与y=f(x) 象的交点为(x1,y1),(x2,y2),(xm,ym),则()(A)0 (B)m (C) 2m (D) 4m【答案】B【解析】都关于对称,它们交点也关于对称,当为偶数时,其和为,当为奇数时,其和为,故选B【命题意】本类题通常主要考查以二次函数为载体考查函数象、对称性、单调性及最值【考试方向】这类试题在考查题型上,通常基本以选择题或填空题的形式出现,往往与函数的定义域、值域、单调性、最值、方程解或函数零点的个数、解不等式性质等数学知识结合,难度为容易题题、中档题、也有有难题【难点中心】若题目为关于某个函数的二次函数单调性、值域、最值或零点个数问题或可化为关某个函数的方程解得个数问题,通常用换元法,转化为一元二次函数或一元二次方程在某个范围上的问题,利用一元二次函数的象与性质求解,注意新变量的取值范围,对含参数的一元二次函数的最值问题,
3、注意分类讨论结合象处理III理论基础解题原理考点一二次函数的概念与表示1概念:形如:函数叫二次函数;2表达形式有:(1)一般式:(2)顶点式:若为抛物线的顶点坐标,(3)截距式:设为抛物线与轴交点的横坐标,则考点二二次函数象与性质解析式f(x)ax2bxc(a0)f(x)ax2bxc(a0)象定义域(,)(,)值域单调性在x上单调递减;在x上单调递增在x上单调递减;在x上单调递增对称性函数的象关于x对称考点三二次函数象与性质的应用 1一元二次方程的实根分布,是一元二次方程=0的根,设=根的分布充要条件充要条件1充要条件2,(,+)且,(-,)且对一元二次方程根的分别问题,结合对应函数的象,考虑对称轴、判别式、端点函数值IV题型攻略深度挖掘【考试方向】这类试题在考查题型上,通常基本以选择题或填空题的形式出现,往往与分段函数、复合函、方程、不等式等数学知识结合考查函数的值域、零点个数或方程解得个数,难度为中档或中档以上【技能方法】解决此类问题通过分类整合结合化为分段函数,结合函数象与性质解题,转化化归思想、分类整合思想、数形结合思想是解题的法宝【易错指导】(1)对二次项系数含参数的问题,要
4、分二次项系数大于0小于0两类,结合对应象处理;(2)对可化为含参数的二次函数在某个区间上的最值问题,要根据对称轴在区间左、中、右分类结合象求解;(3)在用换元法化为二次函数或二次方程问题时,注意新变量的取值范围(4)对一元二次方程根的分别问题,结合对应函数的象,考虑对称轴、判别式、端点函数值V举一反三触类旁通考向1二次函数概念与表示【例1】【福建三明一中模拟】如(1)所示,E为矩形ABCD的边AD上一点,动点P、Q同时从点B出发,点P以1cm/秒的速度沿折线BE-ED-DC运动到点C时停止,点Q以2cm/秒的速度沿BC运动到点C时停止设P、Q同时出发t秒时,BPQ的面积为ycm2已知y与t的函数关系象如(2)(其中曲线OG为抛物线的一部分,其余各部分均为线段),则下列结论:;当时,;当秒时,;当的面积为时,时间的值是或;其中正确的结论是()A B C D【答案】D【解析】根据(2)可得,当点P到达点E时点Q到达点C,ADBC,EBQ=AEB,PF=PBsinEBQ=t,当0t5时,故正确,如3,当t=6秒时,点P在BE上,点Q静止于点C处在ABE与PQB中,AE=BP,EBQ=AEB,
《高考专题二次函数-精品之高中数学(理)黄金100题--- 精校解析Word版》由会员刚**分享,可在线阅读,更多相关《高考专题二次函数-精品之高中数学(理)黄金100题--- 精校解析Word版》请在金锄头文库上搜索。

浙江省宁波五校联盟2023-2024学年高二下学期4月期中联考政治Word版

江苏省无锡市江阴市四校联考2023-2024学年高一下学期4月期中生物试题(原卷版)
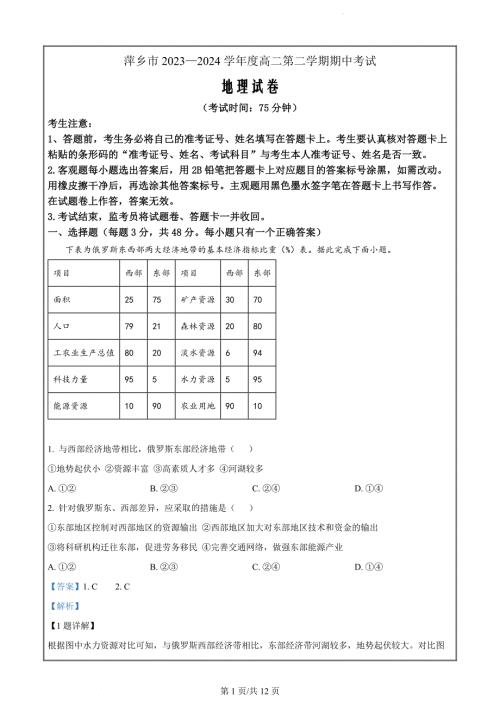
江西省萍乡市2023-2024学年高二下学期4月期中地理试题(解析版)

浙江省宁波金兰联盟2023-2024学年高二下学期4月期中物理试题(原卷版)

广东省珠海市六校2023-2024学年高二下学期4月期中考试数学试题(解析版)

广东省珠海市六校2023-2024学年高二下学期期中学业质量监测政治试题(解析版)

广东省深圳市7校联考2023-2024学年高二下学期期中历史试题(原卷版)

浙江省宁波金兰联盟2023-2024学年高二下学期4月期中物理试题(解析版)

基本数据结构-浙江省2023届高三信息技术选考复考点突破Word版

江苏省无锡市江阴市四校联考2023-2024学年高一下学期4月期中生物试题(解析版)

江苏省无锡市江阴市四校联考2023-2024学年高一下学期4月期中考试历史试题(解析版)

山东省青岛市黄岛区2023-2024学年高二下学期期中考试历史试题(解析版)

浙江省绍兴市上虞区2023-2024学年高二上学期期末化学试题 Word版含解析

河南省开封市五校2023-2024学年高一下学期4月期中联考语文Word版

广东省广州大学附属中学2022-2023学年高二上学期期末考试化学试题(原卷版)

2024届河北省部分高中高三下学期二模物理试题(解析版)

广东省清远市三校2023-2024学年高一下学期4月期中联合考试数学试题(原卷版)

2024届河北省部分学校高三二模语文试题(原卷版)

江苏省无锡市江阴市四校联考2023-2024学年高一下学期4月期中考试历史试题(原卷版)

广东省广州市天河区2023-2024学年高二上学期期考试末化学试卷(无答案)
 2023-2024学年江苏省南京市玄武区八年级(下)期中数学试卷(含解析)
2023-2024学年江苏省南京市玄武区八年级(下)期中数学试卷(含解析)
2024-05-06 23页
 【高中、中学通用】班主任工作手册
【高中、中学通用】班主任工作手册
2024-05-05 77页
 2023-2024学年江苏省南京市六校联合体高一(下)期中物理试卷(含解析)
2023-2024学年江苏省南京市六校联合体高一(下)期中物理试卷(含解析)
2024-04-28 15页
 四种方法计算根号107的近似值
四种方法计算根号107的近似值
2024-04-23 3页
 浙江省丽水市丽水发展共同体联盟2023-2024学年高一下学期4月月考地理试题 Word版含解析
浙江省丽水市丽水发展共同体联盟2023-2024学年高一下学期4月月考地理试题 Word版含解析
2024-04-22 18页
 浙江省培优联盟2023-2024学年高一下学期4月联考数学试题 Word版含解析
浙江省培优联盟2023-2024学年高一下学期4月联考数学试题 Word版含解析
2024-04-22 14页
 浙江省培优联盟2023-2024学年高二下学期4月联考地理试题 Word版含解析
浙江省培优联盟2023-2024学年高二下学期4月联考地理试题 Word版含解析
2024-04-22 18页
 浙江省培优联盟2023-2024学年高二下学期4月联考数学试题 Word版含解析
浙江省培优联盟2023-2024学年高二下学期4月联考数学试题 Word版含解析
2024-04-22 15页
 1.2.4.4伽利略对自由落体运动的研究
1.2.4.4伽利略对自由落体运动的研究
2024-02-29 2页
 1.2.3匀变速直线运动的推论
1.2.3匀变速直线运动的推论
2024-02-29 5页

