
偏微分方程简明教程
33页1、偏微分方程 浙江大学 2008.9 - 2008.12 主要内容: 一、一阶方程 二、二阶方程 椭圆型方程 (典型的例子:Laplace方程) 抛物型方程 (典型的例子:热传导方程;Li-Yaus Harnack inequality) 双曲型方程 (典型的例子:波动方程) 三、特征流形的Cauchy问题:Cauchy-Kowalevski定理 四、无解的线性方程H. Lewy例子。 习题: 必做; 思考题; Open problems。 参考书: F. John, Partial Diff erential Equations, Springer-Verlag, 1982. 谷超豪,李大潜等人,数学物理方程,高教出版社,2002年。 姜礼尚,孔德兴等人,应用偏微分方程,高教出版社,2008年。 1 绪 言 1.基本概念 偏微分方程(PDE) 关于函数u(x,y,)的PDE是形如 F(x,y, ,u,ux,uy, ,uxx,uxy,) = 0(1) 的关系式,其中F是自变量x,y, ,未知函数u以及u的:有 : 限多个偏导数的已知函数。 解(solution): 称u是(1)的 : 解
2、,如果把u(x,y,)及其相应的偏导数代入(1)式后,在x,y, 空间的 某个区域中(1)式关于这些变量恒等地成立。 除非有相反的说明,在本课程中我们总是要求x,y,是实的,u以及在方程(1)中 出现的u的偏导数在实空间的区域中都是关于x,y,的连续函数。为了简单起见,我 们有时也常常省略区域的明确描述,而把所述的命题也“局部地”适用于x,y,空 间中一点的某一适当领域。 偏微分方程组(PDEs): 涉及一个或几个未知函数及其偏导数的多个偏微分方程组成一个方程组。 记n为未知函数的个数,m为PDE的个数 当n m时,此时方程组称为欠定的(under-determined); 当n 0常数),(5) 其中u = u(t,x1, ,xn)。 n = 1 : 弦的振动,波在管中的传播波,c表示传播速度。 n = 2 : 浅水面上的水波。 n = 3 : 声波或光波。 例3. Maxwell 方程(Maxwell equations) 在真空中且无自由电荷和电流的情况下,关于电场强度向量E = E(E1,E2,E3)及磁 场强度向量H = (H1,H2,H3)的Maxwell方 . 程 . 实
3、质上是由六个一阶方程所组成的线性方 程组 Et= curlH, Ht= curlE, divE = divH = 0, (6) 其中, 是描述电磁介质的常数,分别称为真空介电常数和导磁系数。特别地,作为关 系式 Et= curlH,Ht= curlE 的推论,如果t = 0时,关系式 divE = divH = 0 成立,则上式对所有的t均成立。不难验证,这里的每个分量Ei,Hk均满足具有c2= 1/的波动方程(5)。事实上,在方程组中消去磁场强度便得到电场强度的偏微分方 程:这只需对(6)式中的第二式求旋度,再用其第四式可得 curl(curlE) = (curlH)t= Ett, 4 又因为 curl(curlE) = (divE) E, 再利用(6)式中的第三式得到 Ett= ()1E. 类似地,我们可以得到磁场强度向量H所满足的偏微分方程。 例4. 在经典弹性理论中,弹 . 性 . 波 . 可由线性方程组 2ui t2 = ui+ ( + ) xi (divu)(i = 1,2,3)(7) 描述,其中ui(t,x1,x2,x3)是位移向量u的分量,是密度,而,是弹性材料的Lam
4、e常 数。可以证明,每一个分量ui都满足由两个不同的波动算子所组成的四阶方程 ? 2 t2 + 2 ? 2 t2 ui= 0.(8) 当弹 . 性 . 平衡(即ut= 0)时,我们便得到重 . 调 . 和 . 方 . 程 . 2u = 0.(9) 例5. 当密度和比热都是常数时,导热体中的温度分布满足热 . 传 . 导 . 方 . 程 . ut= ku,(10) 其中k 0是常数,表示介质的热传导系数。 例6. 在势能为V (x,y,z)的场中,运动的质量为m的单个质点所满足的Schr odinger方 程是 it= 2 2m() + V , (11) 其中h = 2 是Planck常数。 例7. Tricomi方程 uxx= xuyy.(12) 另一类重要的方程是 uxx= yuyy. 5 这两类方程在平面跨音速流的研究中具有十分重要的作用。 上述例子中的方程都是 : 线:性:的。:非:线 : 性方程也是常见的,但是求解非线性方程实际 上更为困难,因此在实际中常用线性方程近似的表示它们。下面是几个非线性方程的 例子。 例8. 3维Euclid空间中的极 . 小 . 曲 . 面 . z
《偏微分方程简明教程》由会员suns****4568分享,可在线阅读,更多相关《偏微分方程简明教程》请在金锄头文库上搜索。

土地管理与地籍测量---第八章界址点测量
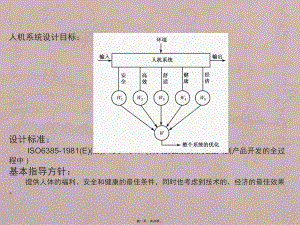
人机工程学案例分析(2)

工程安全培训_201303

第9章房地产投资决策分析

第2章房地产经纪制度

ACM程序设计-东北林业大学acm05

《亲爱的汉修先生》读书交流会

中原_深圳新世界尖岗山项目市场汇报_40P_2012年_别墅_项目分析_量价走势

五年级数学质量分析演示文稿

人工智能小镇-智慧小镇建设20180525

景观基本知识及发展历程

建设工程信息管理(2)

机电驱动技术第二章步进驱动技术
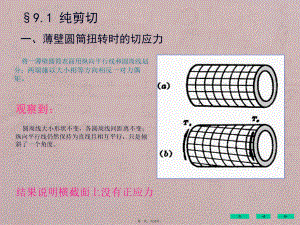
工程力学-第9章圆轴扭转时的应力变形分析与强度刚度设计

第一章第二节幼儿园文化环境建设的原则

第一章检测技术的基础知识

第一章__现代表面工程技术

第六章钢结构工程

第9节项目试运行管理

班主任工作经验交流课件(4)
 天津大学22春《经济法》综合作业二答案参考41
天津大学22春《经济法》综合作业二答案参考41
2024-01-01 16页
 东北农业大学21春《环境法》在线作业三满分答案55
东北农业大学21春《环境法》在线作业三满分答案55
2022-10-06 14页
 中国医科大学21春《卫生法律制度与监督学》在线作业二满分答案5
中国医科大学21春《卫生法律制度与监督学》在线作业二满分答案5
2024-02-15 15页
 简单51单片机数字时钟设计
简单51单片机数字时钟设计
2022-08-08 10页
 东北大学21春《土木工程材料》在线作业二满分答案26
东北大学21春《土木工程材料》在线作业二满分答案26
2023-02-24 13页
 大连理工大学2021年2月《商业银行经营管理》作业考核试题6答案参考
大连理工大学2021年2月《商业银行经营管理》作业考核试题6答案参考
2023-12-26 7页
 吉林大学21秋《计算机可视化编程》在线作业二答案参考25
吉林大学21秋《计算机可视化编程》在线作业二答案参考25
2022-12-23 14页
 比例的意义教学反思
比例的意义教学反思
2023-02-21 4页
 优秀机械工程师设计时需要考虑的因素
优秀机械工程师设计时需要考虑的因素
2023-09-10 7页
 东北农业大学22春《证券投资学》综合作业二答案参考56
东北农业大学22春《证券投资学》综合作业二答案参考56
2023-08-28 14页

