
离散数学考试试题(A、B卷及答案)
6页1、离散数学考试试题(A卷及答案)一、证明题(10分)1) (PQAC)(APQC) (A(PQ)C。PQ=(p-Q)合取(Q-p)证明: (PQAC)(APQC)(PQAC)(APQC)(PQA)(APQ)C反用分配律(PQA)(APQ)C( A(PQ)(PQ)C再反用分配律( A(PQ)C(A(PQ)C2) (PQ) PQ。证明:(PQ)(PQ)(PQ)PQ。二、 分别用真值表法和公式法求(P(QR)(P(QR)的主析取范式与主合取范式,并写出其相应的成真赋值和成假赋值(15分)。主析取范式与析取范式的区别:主析取范式里每个括号里都必须有全部的变元。主析取范式可由 析取范式经等值演算法算得。证明:公式法:因为(P(QR)(P(QR)(PQR)(P(QR)(QR)(PQR)(PQ)(PR)(QR)分配律(PQR)(PQQ)(PQR)(PRQ)(PRR)(PQR)(PQR)(PQR)使(非P析取Q析取R)为0所赋真值,即100,二进制为4所以,公式(P(QR)(P(QR)为可满足式,其相应的成真赋值为000、001、010、011、111:成假赋值为:100、101、110。真值表法:P
2、Q RQRP(QR)P(QR)(P(QR)(P(QR)0 0 00 0 10 1 00 1 11 0 01 0 11 1 01 1 110011001111101111111100111110001由真值表可知,公式(P(QR)(P(QR)为可满足式,其相应的成真赋值为000、001、010、011、111:成假赋值为:100、101、110。三、推理证明题(10分)1)PQ,QR,RSPS。证明:(1)P 附加前提(2)PQ P(3)Q T(1)(2),I(析取三段论)(4)QR P(5)R T(3)(4),I(析取三段论)(6)RS P(7)S T(5)(6),I(假言推理)(8)PS CP2) x(P(x)Q(y)R(x),$xP(x)Q(y)$x(P(x)R(x)证明(1)$xP(x)(2)P(a)(3)x(P(x)Q(y)R(x)(4)P(a)Q(y)R(a)(5)Q(y)R(a)(6)Q(y)(7)R(a)(8)P(a)(9)P(a)R(a)(10)$x(P(x)R(x)(11)Q(y)$x(P(x)R(x)五、已知A、B、C是三个集合,证明(AB)C(AC)(BC) (1
《离散数学考试试题(A、B卷及答案)》由会员re****.1分享,可在线阅读,更多相关《离散数学考试试题(A、B卷及答案)》请在金锄头文库上搜索。

工会基础知识汇总

小学生学习习惯调查问卷

公司员工守则(标准版)

城市社区管理试卷及答案

毕业设计论文-园路与铺装工程-课程论文

职业教育问题与未来发展方向

2022年煤矿防治水安全信息报告制度

整理版新课标全国版课时作业5

手册公司信息系统内控手册信息部

踏春作文600字

新人教版七年级下数学的导学案

金融房屋租赁合同范本.doc

2023年银行从业资格考试公共基础复习资料
10以内三连加减法共15页

一年来的履职情况报告

初中生物教师工作计划标准范本(二篇).doc

【精品】全国中考数学压轴题解析汇编及答案粤闽桂海川滇黔省会
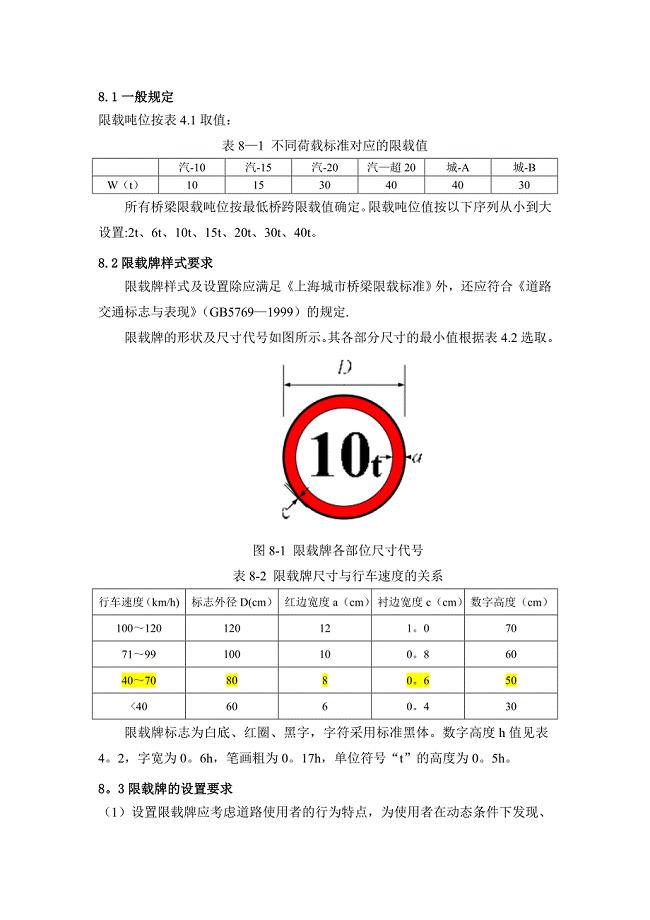
桥梁限载标志设置

安全生产工作档案及管理制度样本(四篇).doc

晚婚婚假申请书
 2019年说明与检测新变化——化学
2019年说明与检测新变化——化学
2023-04-01 16页
 大连理工大学21春《ACAD船舶工程应用》在线作业二满分答案_2
大连理工大学21春《ACAD船舶工程应用》在线作业二满分答案_2
2023-07-20 15页
 2022年07月贵州省贵阳医学院附属医院招聘药剂科人员笔试参考题库(答案解析)
2022年07月贵州省贵阳医学院附属医院招聘药剂科人员笔试参考题库(答案解析)
2023-09-01 75页
 2023年湖北省襄阳市南漳县东巩镇太坪村社区工作人员考试模拟试题及答案
2023年湖北省襄阳市南漳县东巩镇太坪村社区工作人员考试模拟试题及答案
2022-10-31 81页
 福建师范大学21春《城镇体系规划》离线作业2参考答案17
福建师范大学21春《城镇体系规划》离线作业2参考答案17
2022-07-20 12页
 2023年山东省临沂市沂南县铜井镇朝阳村社区工作人员考试模拟题含答案
2023年山东省临沂市沂南县铜井镇朝阳村社区工作人员考试模拟题含答案
2023-12-14 21页
 南开大学21春《证券投资》离线作业2参考答案33
南开大学21春《证券投资》离线作业2参考答案33
2022-11-02 11页
 2023年安全监察人员-环境保护监察员考试参考题库附带答案
2023年安全监察人员-环境保护监察员考试参考题库附带答案
2023-10-04 4页
 2022教师招聘-中学教师招聘考前拔高名师测验卷38(附答案解析)
2022教师招聘-中学教师招聘考前拔高名师测验卷38(附答案解析)
2022-10-08 5页
 2023年山西省晋中市榆次区修文镇陈侃村社区工作人员考试模拟试题及答案
2023年山西省晋中市榆次区修文镇陈侃村社区工作人员考试模拟试题及答案
2024-01-25 81页

