
离散数学第七章图的基本概念知识点总结
13页1、 图论部分第七章、图的基本概念7.1 无向图及有向图无向图与有向图多重集合: 元素可以重复出现的集合无序积: A&B=(x,y) | xAyB 定义 无向图G=, 其中(1) 顶点集V,元素称为顶点(2) 边集E为V&V的多重子集,其元素称为无向边,简称边.例如, G=如图所示, 其中V=v1, v2, ,v5, E=(v1,v1), (v1,v2), (v2,v3), (v2,v3), (v2,v5), (v1,v5), (v4,v5) ,定义 有向图D=, 其中(1) V同无向图的顶点集, 元素也称为顶点(2) 边集E为VV的多重子集,其元素称为有向边,简称边.用无向边代替D的所有有向边所得到的无向图称作D的基图,右图是有向图,试写出它的V和E 注意:图的数学定义与图形表示,在同构(待叙)的意义下是一一对应的 通常用G表示无向图, D表示有向图, 也常用G泛指无向图和有向图, 用ek表示无向边或有向边.V(G), E(G), V(D), E(D): G和D的顶点集, 边集.n 阶图: n个顶点的图有限图: V, E都是有穷集合的图零图: E= 平凡图: 1 阶零图空图: V= 顶点
2、和边的关联与相邻:定义 设ek=(vi,vj)是无向图G=的一条边, 称vi,vj为ek的端点, ek与vi ( vj)关联. 若vi vj, 则称ek与vi ( vj)的关联次数为1;若vi = vj, 则称ek为环, 此时称ek与vi 的关联次数为2; 若vi不是ek端点, 则称ek与vi 的关联次数为0. 无边关联的顶点称作孤立点.定义 设无向图G=, vi,vjV, ek,elE, 若(vi,vj) E, 则称vi,vj相邻; 若ek,el至少有一个公共端点, 则称ek,el相邻.对有向图有类似定义. 设ek=vi,vj是有向图的一条边,又称vi是ek的始点, vj是ek的终点, vi邻接到vj, vj邻接于vi.邻域和关联集顶点的度数设G=为无向图, vV, v的度数(度) d(v): v作为边的端点次数之和 悬挂顶点: 度数为1的顶点 悬挂边: 与悬挂顶点关联的边 G的最大度D(G)=maxd(v)| vV G的最小度d(G)=mind(v)| vV例如 d(v5)=3, d(v2)=4, d(v1)=4,D(G)=4, d(G)=1,v4是悬挂顶点, e7是悬挂边, e1
3、是环 设D=为有向图, vV, v的出度d+(v): v作为边的始点次数之和 v的入度d-(v): v作为边的终点次数之和 v的度数(度) d(v): v作为边的端点次数之和 d(v)= d+(v)+ d-(v)D的最大出度D+(D), 最小出度d+(D) 最大入度D-(D), 最小入度d-(D) 最大度D(D), 最小度d(D) 例如 d+(a)=4, d-(a)=1, d(a)=5, d+(b)=0, d-(b)=3, d(b)=3, D+(D)=4, d+(D)=0, D-(D)=3, d-(D)=1, D(D)=5, d(D)=3. 握手定理定理 任意无向图和有向图的所有顶点度数之和都等于边数的2倍, 并且有向图的所有顶点入度之和等于出度之和等于边数.证 G中每条边(包括环)均有两个端点,所以在计算G中各顶点度数之和时,每条边均提供2度,m条边共提供2m度. 有向图的每条边提供一个入度和一个出度, 故所有顶点入度之和等于出度之和等于边数. 图的度数列设无向图G的顶点集V=v1, v2, , vnG的度数列: d(v1), d(v2), , d(vn)如右图度数列:4,4,2,1
4、,3设有向图D的顶点集V=v1, v2, , vnD的度数列: d(v1), d(v2), , d(vn)D的出度列: d+(v1), d+(v2), , d+(vn)D的入度列: d-(v1), d-(v2), , d-(vn)如右图度数列:5,3,3,3 出度列:4,0,2,1 入度列:1,3,1,2例1 (3,3,3,4), (2,3,4,6,8)能成为图的度数列吗?解 不可能. 它们都有奇数个奇数.例2 已知图G有10条边, 4个3度顶点, 其余顶点的度数均小于等于2, 问G至少有多少个顶点? 解 设G有n个顶点. 由握手定理, 43+2(n-4)210解得 n8例3 证明不存在具有奇数个面且每个面都具有奇数条棱的多面体.证 用反证法. 假设存在这样的多面体, 作无向图G=, 其中V=v | v为多面体的面, E=(u,v) | u,vV u与v有公共的棱 uv. 根据假设, |V|为奇数且vV, d(v)为奇数. 这与握手定理的推论矛盾.多重图与简单图定义 (1) 在无向图中,如果有2条或2条以上的边关联同一对顶点, 则称这些边为平行边, 平行边的条数称为重数.(2)在有向图
《离散数学第七章图的基本概念知识点总结》由会员n****分享,可在线阅读,更多相关《离散数学第七章图的基本概念知识点总结》请在金锄头文库上搜索。

项目二财务管理价值观念

山东省安全生产风险分级管控与隐患排查治理信息化系统交流材料-2018.9.26

人教版高中地理必修3第一章地理环境与区域发展第二节《地理信息技术在区域地理环境研究中的应用》

第三章2房地产抵押贷款-固定利率抵押贷款
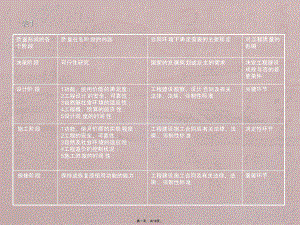
第八章工程质量法律制度

第25讲家庭电路与安全用电

餐厅点餐系统项目

项目7水箱水位控制

框架完整个人年度工作总结范文模板

科目名称-国土交通省

金融工程09课件

高校自主招生之结构化面试

房地产私募股权投资基金(PE)专题研究.

房地产基础知识培训2012

第一章食品检测技术基础知识

第10章网站设计与建设综合实例

第5章尝试迷人的机器人项目机器人灭火项目

自考英语二unit3

企业人力资源管理师第六章劳动法与劳动关系管理

第三章市场营销宏观环境分析
 学校课间操活动计划
学校课间操活动计划
2024-02-03 4页
 十月份工作总结
十月份工作总结
2023-08-02 8页
 “一苇渡江”与“吃肉边菜”-- 两个著名禅宗故事的历史探究文库
“一苇渡江”与“吃肉边菜”-- 两个著名禅宗故事的历史探究文库
2023-03-21 12页
 东北师范大学21春《儿童文学》在线作业二满分答案93
东北师范大学21春《儿童文学》在线作业二满分答案93
2023-12-20 16页
 矛和盾的集合教学设计
矛和盾的集合教学设计
2023-03-29 6页
 东北农业大学21春《农业经济学》在线作业二满分答案65
东北农业大学21春《农业经济学》在线作业二满分答案65
2022-09-02 15页
 让生态更自然-让生长更自由
让生态更自然-让生长更自由
2023-01-26 7页
 大连理工大学21春《起重机金属结构》在线作业二满分答案5
大连理工大学21春《起重机金属结构》在线作业二满分答案5
2023-01-30 11页
 ERP国内外软件应用与比较
ERP国内外软件应用与比较
2022-12-27 7页
 证券公司代销金融产品业务风险防范操作实务 课后测验
证券公司代销金融产品业务风险防范操作实务 课后测验
2023-06-05 3页

