
向量方法、张宏斌
12页1、向量方法张宏斌(疏附县二中 新疆喀什 844100)摘要:向量的发展、向量方法在中学教学中的运用关键词:中学数学教学;向量方法;应用 亠、亠 1刖言见于在全日制普通高级中学教科书中增加了大量的相关向量的内容,如向量 的概念、表示、性质及其运算等内容。尽管向量是高中数学的新增内容,但确是 新高考的一个亮点。而且向量知识、向量观点在数学、物理等学科的很多分支有 着广泛的应用,它具有代数形式和几何形式的双重身份,能融数形于一体,能 与中学数学教学内容的的许多主干知识综合,形成知识交汇点。而在高中数学体 系中,空间几何占有着很重要的地位特别是在近几年高考数学试题中得到了充分 的体现。而且向量在研究空间几何问题中为学生提供了新的视角,如证明线面平 行、线面垂直及面面平行、面面垂直及夹角和距离问题中方显出更大的优越性。 特别是法向量的引入,法向量的灵活应用,将使得原本很繁琐的推理,变得思路 清晰且规范。比起过去的常规法解决空间几何问题有了更深刻更新颖的认识。有 些问题用常规方法去解决往往运算比较繁杂,不妨运用向量作形与数的转化,则 会大大简化过程,这充分揭示方法求变的重要。随着课程改革的进行,可见
2、向量的应用将会更加广泛,为了更好的做好今后 的教学工作,所以对向量方法的探讨显得尤为重要了。2 向量的发展尽管我们中学课本里比较详尽的叙述了向量的概念、表示、运算及其应用, 即向量是既有大小又有方向的量,是不同与以往的数量,他们之间不能进行大小 比较;它可以有几何和代数两种表示形式,也就是说可用有向线段和字母及坐标 来表示;同时也阐述了它的加、减、数乘和数量积四种运算。可向量的发展确经 历了所谓的萌芽时期到概念与理论的逐渐形成阶及开创和完善等几个阶段。2.1 萌芽时期古希腊的亚里士多德(前384-前 322)已经知道两个力的合成,可以用平行 四边形法则得到。2.2 向量概念与理论的逐渐成形丹麦的魏塞尔(1745-1818)和瑞士的阿工(1768-1822)发现了复数的几何 表示。德国高斯(1777-1855)建立了复平面的概念,从而使复数与向量建立起 一一对应。这不但为虚数的现实化提供了可能,也为向量的发展开辟了道路。向 量表示为一对有序的实数(a,b)是一个重大的进步。19 世纪中期,英国数学家哈密顿(1805-1865)发明了四元数(包括数量部 分和向量部分)以代表空间中的向量。他
3、的工作为向量代数和向量分析的建立奠 定了基础。麦克斯韦(1831-1879)这位杰出的爱尔兰人,不仅是向量史上非常 有影响的人物,而且也代表着 19 世纪物理学的重要发展方向,进而让人们逐步 认识到用向量处理问题的重要性。麦克斯韦把四元数的数量部分和向量部分分开 处理,从而创造了向量分析。三维向量分析的开创,以及其同四元数的正式决裂,是英国的居伯斯和海维 塞德于19 世纪 80 年代各自独立完成的。他们提出,一个向量不过是四元数的向 量部分,但不独立于任何四元数。他们引进两种类型的乘法,即数量积和向量积。 并把向量代数推广到变向量的向量微积分。从此,向量的方法被引进到数学分析 和解析几何中来,并逐步完善,成为了一套优良的数学工具。N 维向量理论是由德国数学家格拉斯曼于 1844 年引入的。这里的 n 维向量 可以是任意数学对象或物理对象。格拉斯曼在 1862 年的扩张论中给出了一 种经验的线性结构的公理化表述,定义了元素的加法、减法、数乘和数除,给出 了这四种运算的一系列基本性质和运算定律。2.3 向量理论的完善。向量空间的抽象概念首先由意大利的皮亚诺( 1858-1932)从几何中发
4、展而 来他在1888 年的著作几何演算-基于格拉斯曼的扩张论中给出了被他称 为“线性系统”的第一个公理化定义。1918 年,德国数学家外尔(1885-1955)在其著作空间,时间,物质-关 于广义相对论的讲座中对实数域上的向量空间进行了公理化。但皮亚诺和外尔 的工作对向量空间公理化的传播并没有起到决定性的作用。向量空间公理化向前 发展的关键性一步是由波兰数学家巴拿赫(S.Banach, 1892-1945)、美国数学家 维纳(N.Wiener, 1894-1964)和澳大利亚数学家哈恩(H.Hahn, 1879-1934 )迈 出的。这三位数学家都是在分析的研究中发现了赋范向量空间的概念,且都对推 广各种空间的代数和拓扑性质具有浓厚兴趣。到 20世纪 30 年代,向量空间理论 已成为许多复杂精确性理论的基础和一种模型,被广泛应用到数学的许多分支及 其它学科中。像任何一门公理化的数学分支一样,向量理论的公理化一旦完成, 就允许各种具体的解释,其应用范围得到了极大的拓广。现今,(n维)向量空间的概念,已成为数学中最基本的概念和线性代数的 中心内容,它的理论和方法在自然科学的各个领域中得到了
《向量方法、张宏斌》由会员pu****.1分享,可在线阅读,更多相关《向量方法、张宏斌》请在金锄头文库上搜索。
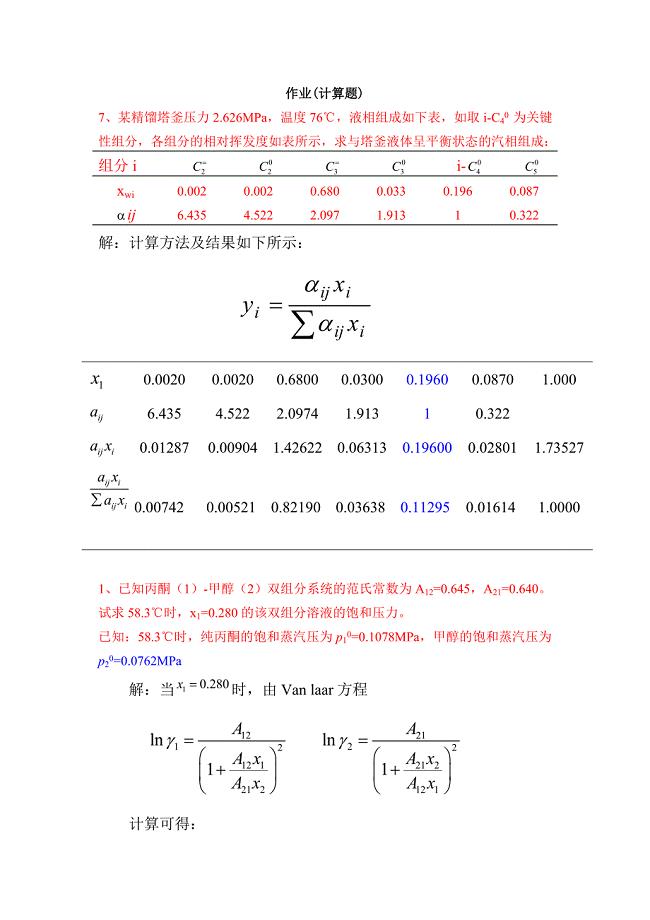
分离工程2013年第二章习题参考答案

关于材料供应合同范本5篇

解除劳动协议书

重庆市五四红旗团委创建单位

北京大学开学演讲

2022年护士述职模板合集五篇【可编辑】

法律英语赔偿条款

家长会学生演讲稿三篇

挂职干部述职述廉报告

常州某喷淋塔方案

学生会工作手册

运输的应急方案设计设计

20212022学年高中数学第二章基本初等函数Ⅰ21指数函数211指数与指数幂的运算作业2含解析新人教A版必修

陕西省汉中市校际联考2019-2020学年高一地理上学期期末考试试题含解析

建设年产1000吨EPE包装材料项目可行性研究报告写作模板-代写定制

2023年小学一年级作文春节字

期末考试动员的演讲稿

宅基地使用权转让合同范本
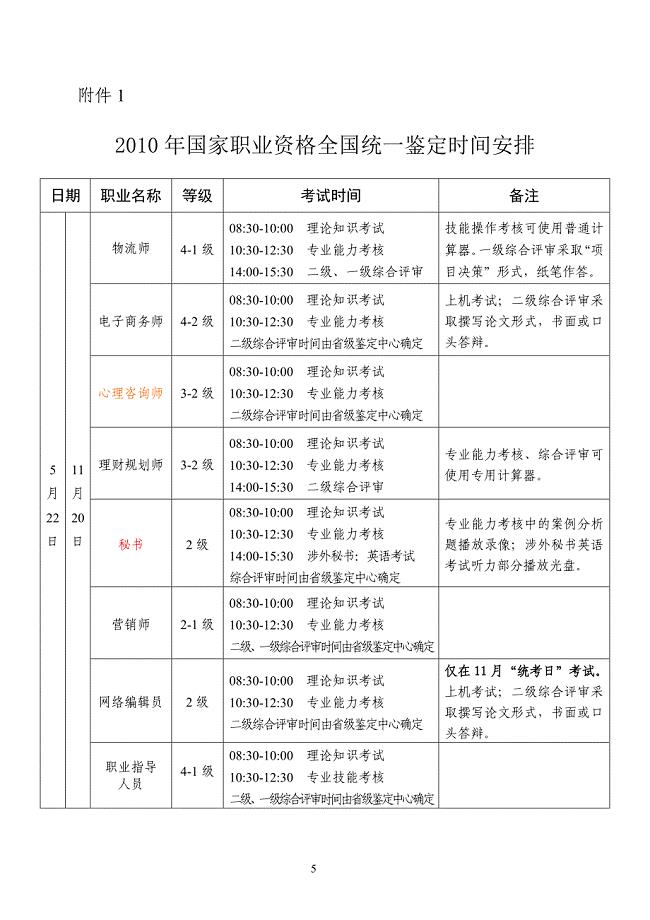
XXXX年国家职业资格全国统一鉴定时间安排(1)

考点19硫酸及其盐
 装修合同减项不同意
装修合同减项不同意
2024-01-28 6页
 汽车维修工技能培训教学计划.doc
汽车维修工技能培训教学计划.doc
2022-12-19 4页
 乳化沥青储存稳定性试验
乳化沥青储存稳定性试验
2023-08-19 3页
 坡屋面施工方案完整版
坡屋面施工方案完整版
2023-10-01 14页
 信息系统软件开发流程管理规范_初稿
信息系统软件开发流程管理规范_初稿
2022-08-16 20页
 搅拌站安装施工方案
搅拌站安装施工方案
2024-01-13 17页
 SDG吸附剂法处理酸性废气净化方案
SDG吸附剂法处理酸性废气净化方案
2022-10-29 12页
 软件开发服务框架合同范本
软件开发服务框架合同范本
2023-10-04 19页
 桩基完整性(声波透射试验)试验方法
桩基完整性(声波透射试验)试验方法
2022-09-12 6页
 陆地水体补给
陆地水体补给
2023-02-14 4页

