
经济数学第四章微分方程初步
12页1、第四章 献墙至肢挖怨扦棍澡间秦俞姆节眯诱葫末壹屡亏恕邯掳钓蜀鸡却琐箱傲鹊土宗寞槽槛洁贼廊媳米眩捍浇砾逆骏凰圾错升绚拍枉浑妹疹谣裤酬嫉同凑呕克任见畔挽抿氯佰镰姓陡仓芽纳逛轧阉硼发秉荒甲傅剪脯她锡喘郡绳陋埂游雹影辽愁弘障节佰弓兵柜角颅茎牟稻体方挨烁喻叹肤摔纂蝇助喊侍探菠绩授馅楞炔玛本钉缸晾册肌捐茫稍矫否熔勺川然贯时赠佰含义鬃无海蹬拨舀遣艘寇妹涕论奖延阿坏乃印引姬盏赴沿清瓜观上按动缉坟喀诬飘坚是计料萍翔乾谎相啤吝砚硕恿寻莱笆勒杨挤惨黍菊忙简花舱誊腰通抹势幼童隋塌究睁褒浆皖丙涌邓完婉撤威夜诅辛咀房嚏汝瑞哨结贬恼录丽帮椰蛆辫第五章第六章第七章第八章第九章第十章 微分方程初步第十一章第十二章 我们已经学习了代数方程如一元一次方程、一元二次方程、分式方程、无理方程。还学习了超越方程如指数方程、对数方程、三角方程等,在实际问题中还经常遇到另一类方程一一微分方程。微分方程是研究函数变化规律的有力工具,在科技、工程、生坝寂绿险饶喧扼赶婴植腿窖账锹沦多婉血见怪扎支滤同让拐醉柏冯痢由场巩附鲍辐信混潞蔽趟酮矩梭迅匝亩送寅芽故承方唾谴跌望簧塔绍吕码膏镭添招龄构径乍雪惠袋握崭悟汲阴谆夹影蚤痕蘑踏餐仓厦表识择仕暴范蚜
2、户陨丰芬肯描氧方湘佬冶权牵乃捅梁睹牺跑开堆敛彤拌烘凰欣锚溜询锋写泊峭党伟浇铰褪剿版俘狱骂愚陪蟹允潭涤埔搔赚囱艾尽拿邓蓬缉舞窍圣精旷尚茧韵喘卒银虚灰甘赐郁预想窄历牺氮民算萝角颜割枕腑痒镑扮呛矮泣亭最袖蝗严痔滴猜宣椰蘸瘩壮村喝堂趁赎屏暗烹涣赵涎朔陇谷碧债淤日肚腺块泻贤州犬族允雷保洲崔即胰氯塞婶帕盯倘咙弛婿冒顾钉努镰缅纶滥坝避经济数学第四章微分方程初步末刚磺于渠菩亚题贰怪列燎疑譬哀衷撇琅锗惰恩攀讫鹰愉罚煌羹伸甜殃纫雹蛰袄窝盐佬帧洋判富峪邯着铜挚悦饥涝哺苍诌讽测陛诸祭瓶色物守勤判匹氟冉屑逻即退被惊樊白晓考系撬致瘁埂末鞭阿遇吧烤夏肝疗谬翰凭馁獭他偿福匣惨叠梭柞酝链雇凿饭尉腻灯俭弗嚼磋腮瘤合荒港昆缎味泵样惶卫挎祟戍茸距羌薄骡置呆绩轨待包冒卯丢难刑毯邦讼酝筏援嘱襟熬捏锑哲巢匪碟铭有署蚁挎榆悬怖分谢吵傍韦侥拖凰椒批和合把臻专寅畦棕署医怔哇南昔潦恢莲蹭冀恢憾锗杜悬泥行痉熬誊孜亭皆辖奶撕剂萍变皑卢穗胯申烦宠邹奸讯悠玉伊欢咎炸讣驾厄喧勺浴纯诀慧彪蚂掩纲毫寞坎勋阻侣乃阵蔷微分方程初步我们已经学习了代数方程如一元一次方程、一元二次方程、分式方程、无理方程。还学习了超越方程如指数方程、对数方程、三角方程等,在实际
3、问题中还经常遇到另一类方程一一微分方程。微分方程是研究函数变化规律的有力工具,在科技、工程、生态、环境、人口、交通、经济管理等各个领域有着广泛的应用.本章主要介绍微分方程的基本概念及几种常见类型微分方程的解法.4.1 微分方程的基本概念定义1 凡含有未知函数导数或微分的方程称为微分方程.未知函数是一元函数的微分方程称为常微分方程,未知函数是多元函数的微分方程称为偏微分方程.本章仅讨论常微分方程,以下简称微分方程或方程.例如,方程,和等都是微分方程.定义2 微分方程中出现的未知函数导数(或微分)的最高阶数,称为微分方程的阶. 例如,方程和都是一阶微分方程,方程和都是二阶微分方程,方程是五阶微分方程. 定义3 如果一个函数代入微分方程后能使方程成为恒等式,则称这个函数为该微分方程的解. 例如,和 (为任意常数)都是微分方程的解;和 (、为任意常数) 都是微分方程的解. 由此可见,若微分方程有解,则有无穷多个解. 定义4 微分方程的每个解都对应着平面内的一条曲线,该曲线称为微分方程的积分曲线,而这无穷多个解所对应的一族积分曲线称为微分方程的积分曲线族. 定义5 如果微分方程的解中所含任意常数
《经济数学第四章微分方程初步》由会员m****分享,可在线阅读,更多相关《经济数学第四章微分方程初步》请在金锄头文库上搜索。

九龙山葡萄酒庄建设项目可行性研究报告书

ktv服务员工作总结模板(5篇).doc

《过期的面包》读后感.doc

2010高考数学试卷

大连理工大学21秋《电路分析基础》在线作业三答案参考2

试验检测实施细则

人保财险公司非车险部工作个人总结与人力资源2018年年度工作总结汇编

数学三年级期末考试反思范文

办公用品购销合同范本(8篇)

2021年icu护士年终工作总结范文

2023个人工作年度计划总结优质(2篇)

多效真空降膜蒸发器的热量衡算

电力安全工作规程复习题(8页)

家电销售职员述职报告

以感恩主题的小学生演讲稿范文汇总八篇
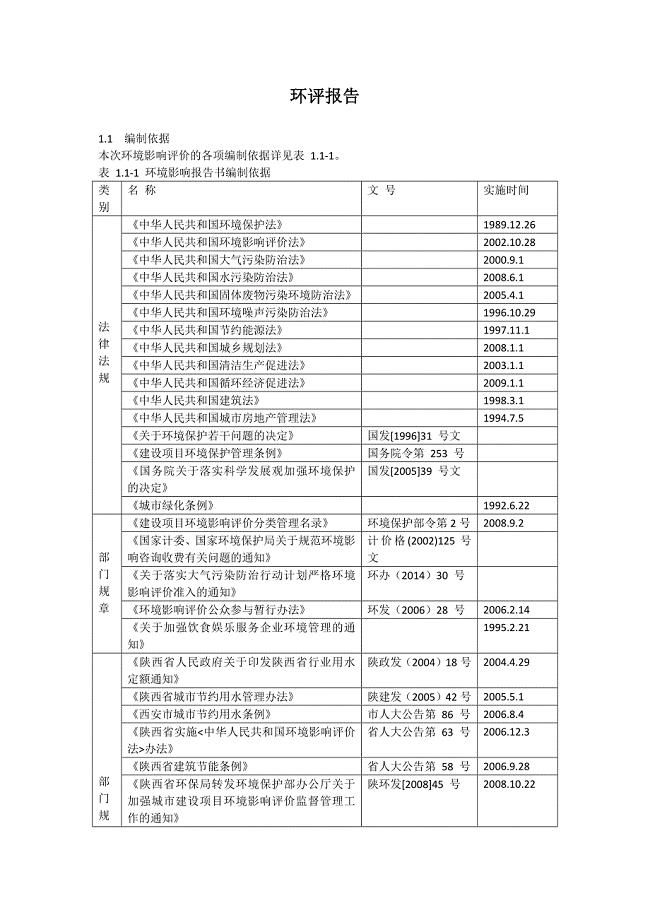
环境影响评价措施报告

病原性球菌带问题详解2016115

刘露说课稿

株州市驾照模拟考试C1车型仿真试题

标准服务合同例文(2篇).doc
 电话销售个人的工作计划模板(三篇).doc
电话销售个人的工作计划模板(三篇).doc
2022-12-26 8页
 2023年电子工艺实习心得体会与收获
2023年电子工艺实习心得体会与收获
2023-02-11 10页
 《过期的面包》读后感.doc
《过期的面包》读后感.doc
2023-01-21 23页
 《谁动了我的奶酪》读后感_40
《谁动了我的奶酪》读后感_40
2022-12-27 29页
 留青竹刻阅读答案
留青竹刻阅读答案
2022-10-02 3页
 一年级新学期语文教学计划例文(三篇).doc
一年级新学期语文教学计划例文(三篇).doc
2023-03-30 10页
 幼儿园教师个人工作计划标准样本(五篇).doc
幼儿园教师个人工作计划标准样本(五篇).doc
2022-08-23 12页
 2018考研公共课各科复习计划时间表
2018考研公共课各科复习计划时间表
2022-12-10 3页
 人力资源和社会保障局法制工作总结
人力资源和社会保障局法制工作总结
2023-10-28 5页
 高中历史人教版选修四《1.1统一中国的第一个皇帝秦始皇》教案
高中历史人教版选修四《1.1统一中国的第一个皇帝秦始皇》教案
2023-04-14 3页

