
离散数学(第十五章)
36页1、1,第十五章 欧拉图与哈密顿图,主要内容 欧拉图 哈密顿图 带权图与货郎担问题,2,第十五章 欧拉图与哈密顿图,预备知识 无向图G = d(v), d+(v), d(v) 奇度顶点与偶度顶点 连通,通路,回路,3,瑞士数学家,最多产的数学家 1100书籍论文 全集75卷 13个孩子 最后17年失明,Question: 如何将左边图所示的七桥问题转换为点和边来描述? 一个游人怎样才能不重复地一次走遍七座桥,最后又回到出发点呢?,Link to the video,Leonhard Euler:17071783,历史背景,4,下面哪些图形可以一笔画,哪些图形不能一笔画?,试一试:,(1),(2),(3),(4),(5),(6),5,(2),(2),(3),(3),6,中途点特征:,笔沿着某条边进去后,必定沿另一条边出去,于是知道与中途点为端点的边必定是成对出现的,这样中途点必定是偶点。,进去,出来,进去,出来,如果起点和终点重合,则与他们相连的边是偶数条,所以也是偶点 起点和终点不重合,与他们相连的边奇数条,则是都是奇点,“一笔画”图形特征:一个图形可以“一笔画”则奇点的个数是0个或2个,
2、7,欧拉图定义,定义15.1 (1) 欧拉通路经过图中每条边一次且仅一次行遍所有顶点的通路. (2) 欧拉回路经过图中每条边一次且仅一次行遍所有顶点的回路. (3) 欧拉图具有欧拉回路的图. (4) 半欧拉图具有欧拉通路而无欧拉回路的图. 几点说明: 规定平凡图为欧拉图. 欧拉通路是生成的简单通路,欧拉回路是生成的简单回路. 环不影响图的欧拉性.,8,上图中,(1) ,(4) 为欧拉图,(2),(5)为半欧拉图,(3),(6)既不是欧拉图,也不是半欧拉图. 在(3),(6)中各至少加几条边才能成为欧拉图?,欧拉图实例,9,无向欧拉图的判别法,定理15.1 无向图G是欧拉图当且仅当G连通且无奇度数顶点. 证 若G 为平凡图无问题. 下设G为 n 阶 m 条边的无向图. 必要性 设C 为G 中一条欧拉回路. (1) G 连通显然. (2) viV(G),vi在C上每出现一次获2度,所以vi为偶度顶点. 由vi 的任意性,结论为真. 充分性 对边数m做归纳法(第二数学归纳法). (1) m=1时,G为一个环,则G为欧拉图. (2) 设mk(k1)时结论为真,m=k+1时如下证明:,10,PL
3、AY,从以上证明不难看出:欧拉图是若干个边不重的圈之并,见示意图3.,11,欧拉图的判别法,定理15.2 无向图G是半欧拉图当且仅当G 连通且恰有两个奇 度顶点. 证 必要性简单. 充分性(利用定理15.1) 设u,v为G 中的两个奇度顶点,令 G =G(u,v) 则G 连通且无奇度顶点,由定理15.1知G 为欧拉图,因而 存在欧拉回路C,令 =C(u,v) 则 为 G 中欧拉通路.,12,下图是某展览厅的平面图,它由五个展室组成,任两展室之间都有门相通,整个展览厅还有一个进口和一个出口,问游人能否一次不重复地穿过所有的门,并且从入口进,从出口出?,练习 1,13,下图是一个公园的平面图.要使游客走遍每条路而不重复,问出入口应设在哪里?,练习 2,14,有向欧拉图的判别法,定理15.3 有向图D是欧拉图当且仅当D是强连通的且每个顶 点的入度都等于出度. 本定理的证明类似于定理15.1. 定理15.4 有向图D是半欧拉图当且仅当D是单向连通的,且 D中恰有两个奇度顶点,其中一个的入度比出度大1,另一个 的出度比入度大1,而其余顶点的入度都等于出度. 本定理的证明类似于定理15.1. 定理
4、15.5 G是非平凡的欧拉图当且仅当G是连通的且为若干 个边不重的圈之并. 可用归纳法证定理15.5.,15,查阅有关欧拉图应用研究的文献 书面总结: 研究动机 研究框架 关键的发现 结论,作业,16,15.2 哈密顿图,历史背景:哈密顿周游世界问题与哈密顿图,(1) (2),17,18,哈密顿图与半哈密顿图,定义15.2 (1) 哈密顿通路经过图中所有顶点一次仅一次的通路. (2) 哈密顿回路经过图中所有顶点一次仅一次的回路. (3) 哈密顿图具有哈密顿回路的图. (4) 半哈密顿图具有哈密顿通路且无哈密顿回路的图. 几点说明: 平凡图是哈密顿图. 哈密顿通路是初级通路,哈密顿回路是初级回路. 环与平行边不影响哈密顿性. 哈密顿图的实质是能将图中的所有顶点排在同一个圈上,19,实例,在上图中, (1),(2) 是哈密顿图; (3)是半哈密顿图; (4)既不是哈密顿图,也不是半哈密顿图,为什么?,20,无向哈密顿图的一个必要条件,定理15.6 设无向图G=是哈密顿图,对于任意V1V且 V1,均有 p(GV1) |V1|,证 设C为G中一条哈密顿回路 (1) p(CV1) |V1| (2
《离散数学(第十五章)》由会员suns****4568分享,可在线阅读,更多相关《离散数学(第十五章)》请在金锄头文库上搜索。

土地管理与地籍测量---第八章界址点测量
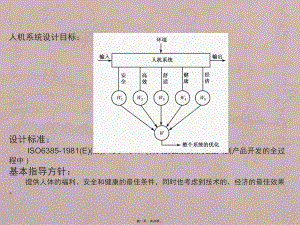
人机工程学案例分析(2)

工程安全培训_201303

第9章房地产投资决策分析

第2章房地产经纪制度

ACM程序设计-东北林业大学acm05

《亲爱的汉修先生》读书交流会

中原_深圳新世界尖岗山项目市场汇报_40P_2012年_别墅_项目分析_量价走势

五年级数学质量分析演示文稿

人工智能小镇-智慧小镇建设20180525

景观基本知识及发展历程

建设工程信息管理(2)

机电驱动技术第二章步进驱动技术
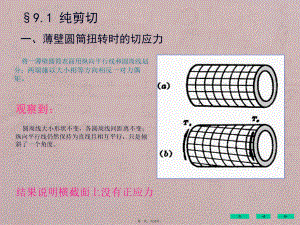
工程力学-第9章圆轴扭转时的应力变形分析与强度刚度设计

第一章第二节幼儿园文化环境建设的原则

第一章检测技术的基础知识

第一章__现代表面工程技术

第六章钢结构工程

第9节项目试运行管理

班主任工作经验交流课件(4)
 优质护理培训课件
优质护理培训课件
2023-12-11 28页
 怎么练好护理操作课件
怎么练好护理操作课件
2023-12-11 28页
 面瘫的治疗与护理课件
面瘫的治疗与护理课件
2023-12-11 27页
 脑卒中患者护理课件模板
脑卒中患者护理课件模板
2023-12-11 31页
 护理反向交班课件
护理反向交班课件
2023-12-11 27页
 护理案例比赛课件题目
护理案例比赛课件题目
2023-12-11 27页
 医院icu护理课件
医院icu护理课件
2023-12-11 33页
 乙肝的护理课件
乙肝的护理课件
2023-12-11 28页
 中药坐浴护理课件
中药坐浴护理课件
2023-12-11 26页
 口腔护理课件题目
口腔护理课件题目
2023-12-11 29页

