
偏导与积分复习
54页1、2019/5/13,1,1. 极限,证明极限不存在的方法:路径法,求极限的方法(坐标变换法),2. 连续,上页 下页 返回,有,3. 偏导数,第八章 多元函数微分法,2019/5/13,2,连续性,偏导数存在,方向导数存在(以后讲),可微性,偏导数连续,5. 微分,4. 偏导数计算:复合函数求偏导,隐函数求偏导, 及其高阶导数,2019/5/13,3,例1. 讨论二重极限,解法1,解法2 令,解法3 令,时, 下列算法是否正确?,上页 下页 返回,2019/5/13,4,分析:,解法1,解法2 令,此法第一步排除了沿坐标轴趋于原点的情况,此法排除了沿曲线趋于原点的情况.,此时极限为 1 .,第二步,未考虑分母变化的所有情况,上页 下页 返回,2019/5/13,5,解法3 令,此法忽略了 的任意性,极限不存在 !,由以上分析可见, 三种解法都不对,因为都不能保证,自变量在定义域内以任意方式趋于原点 .,特别要注意, 在某些情况下可以利用极坐标求极限,但要注意在定义域内 r , 的变化应该是任意的.,同时还可看,到,本题极限实际上不存在 .,上页 下页 返回,2019/5/13,6,证:
2、 利用,故f 在 (0,0) 连续;,知,在点(0,0) 处连续且偏导数存在 , 但不可微 .,例2. 证明:,上页 下页 返回,2019/5/13,7,而,所以 f 在点(0,0)不可微 !,而当,上页 下页 返回,2019/5/13,8,( 有二阶连续偏导数), 求,例3,设,解,上页 下页 返回,2019/5/13,9,上页 下页 返回,2019/5/13,10,上页 下页 返回,例4,2019/5/13,11,有连续的一阶偏导数 ,及,分别由下两式确定,求,又函数,答案:,( 2001考研 ),例5. 设,上页 下页 返回,2019/5/13,12,设,则,两边对 x 求偏导,上页 下页 返回,例6. 设,2019/5/13,13,例7. 设,其中 f 与F分别具,解;方程两边对 x 求导, 得,有一阶导数或偏导数, 求,(99 考研),上页 下页 返回,(用隐函数求导公式),2019/5/13,14,例8.设,有二阶连续偏导数, 且,求,解:,上页 下页 返回,2019/5/13,15,6.几何应用,(1)空间曲线切线及法平面,上页 下页 返回,切向量,(2)曲面的切平面与法
3、线,2019/5/13,16,7.方向导数与梯度,(1)定义,上页 下页 返回,(2)公式,(3)梯度,2019/5/13,17,8.极值,(1) 无条件极值,第一步 利用必要条件在定义域内找驻点.,即解方程组,第二步 利用充分条件 判别驻点是否为极值点 .,(2) 条件极值,(1) 简单问题用代入法,如对二元函数,(2) 一般问题用拉格朗日乘数法,上页 下页 返回,2019/5/13,18,设拉格朗日函数,如求二元函数,下的极值,解方程组,第二步 判别, 比较驻点及边界点上函数值的大小, 根据问题的实际意义确定最值,第一步 找目标函数, 确定定义域 ( 及约束条件),9. 最值,在条件,求驻点 .,上页 下页 返回,2019/5/13,19,例9.,函数,在点,处的梯度,解:,则,注意 x , y , z 具有轮换对称性,(92考研),目录 上页 下页 返回 结束,2019/5/13,20,指向 B( 3, 2 , 2) 方向的方向导数是 .,在点A( 1 , 0 , 1) 处沿点A,例10. 函数,提示:,则,(96考研),目录 上页 下页 返回 结束,2019/5/13,21,例
4、11 曲面,在任一点处的切平面( ).,则,故切平面的法向量为,A.垂直于一定直线; B.平行于一定平面;,C.与一坐标平面成定角; D.平行于一定直线.,所以,应选D.,解:设,又,故切平面平行于以,为方向向量的直线.,2019/5/13,22,例12.,求曲线,对应点处的切线方程和法平面方程.,切线方程,法平面方程,即,解: 由于,对应的切向量为,在, 故,上页 下页 返回,时, x(0) = 0, y(0) = 1, z(0) = 2. 又,2019/5/13,23,例13.,求函数,解: 第一步 求驻点.,得驻点: (1, 0) , (1, 2) , (3, 0) , (3, 2) .,第二步 判别.,在点(1,0) 处,为极小值;,解方程组,的极值.,求二阶偏导数,目录 上页 下页 返回 结束,2019/5/13,24,在点(3,0) 处,不是极值;,在点(3,2) 处,为极大值.,在点(1,2) 处,不是极值;,目录 上页 下页 返回 结束,2019/5/13,25,例14.,求旋转抛物面,与平面,之间的最短距离.,解:,设,为抛物面,上任一点,,则 P,的距离为,问题归结
《偏导与积分复习》由会员n****分享,可在线阅读,更多相关《偏导与积分复习》请在金锄头文库上搜索。

项目二财务管理价值观念

山东省安全生产风险分级管控与隐患排查治理信息化系统交流材料-2018.9.26

人教版高中地理必修3第一章地理环境与区域发展第二节《地理信息技术在区域地理环境研究中的应用》

第三章2房地产抵押贷款-固定利率抵押贷款
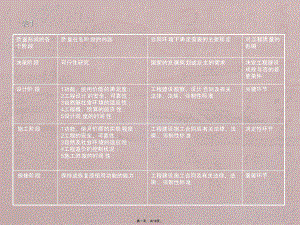
第八章工程质量法律制度

第25讲家庭电路与安全用电

餐厅点餐系统项目

项目7水箱水位控制

框架完整个人年度工作总结范文模板

科目名称-国土交通省

金融工程09课件

高校自主招生之结构化面试

房地产私募股权投资基金(PE)专题研究.

房地产基础知识培训2012

第一章食品检测技术基础知识

第10章网站设计与建设综合实例

第5章尝试迷人的机器人项目机器人灭火项目

自考英语二unit3

企业人力资源管理师第六章劳动法与劳动关系管理

第三章市场营销宏观环境分析
 优质护理培训课件
优质护理培训课件
2023-12-11 28页
 怎么练好护理操作课件
怎么练好护理操作课件
2023-12-11 28页
 面瘫的治疗与护理课件
面瘫的治疗与护理课件
2023-12-11 27页
 脑卒中患者护理课件模板
脑卒中患者护理课件模板
2023-12-11 31页
 护理反向交班课件
护理反向交班课件
2023-12-11 27页
 护理案例比赛课件题目
护理案例比赛课件题目
2023-12-11 27页
 医院icu护理课件
医院icu护理课件
2023-12-11 33页
 乙肝的护理课件
乙肝的护理课件
2023-12-11 28页
 中药坐浴护理课件
中药坐浴护理课件
2023-12-11 26页
 口腔护理课件题目
口腔护理课件题目
2023-12-11 29页

