
插值和拟合.
18页1、 插值和拟合的定义1.定义: 若x为自变量,y为因变量,则x与y之间有一个确定的函数表达式f(x),现实中,这个函数关系式很难确定,运用逼近的方法处理:取得一组数据点(xi,yi,i=1,2,3.n),构造一个简单函数p(x)作为f(x)的近似表达式,且p(x)满足: p(xi)=f(xi)=yi i=1,2,3,4.n这就是插值问题。 若不要求p(x)通过所有数据点,而是要求曲线在某种准则下整体与数据点接近,例如运用最小二乘法得到p(x),这种问题称为拟合。2插值类型:一维插值是指对一维函数y=f(x)进行插值,二维插值就是对二维函数y=f(x,y)进行插值.3. 插值的matlab函数及其应用(1) .一维插值:yi=interp1(x,Y,xi,method),对一组节点(x,Y)进行插值,计算插值点xi的函数值。method包括了一下几种类型:Nearest:线性最邻近插值(速度最快,平滑性最差)Linear:线性插值(默认项)(生成效果连续,但是顶点处有坡度变化)Spline:三次样条插值(运行时间较长,插值数据和导数均连续)Pchip:分段三次艾米尔特(hermite)插值
2、Cubic:双三次插值(较高版本的matlab不能运用,v5cubic能够运行)运行的代码及插值效果:clear;clc;x=0:0.2:2;y=(x.2-3*x+5).*exp(-3*x).*sin(x);xi=0:0.03:2;yi_nearest=interp1(x,y,xi,nearest);yi_linear=interp1(x,y,xi,linear);yi_spline=interp1(x,y,xi,spline);yi_pchip=interp1(x,y,xi,pchip);yi_cubic=interp1(x,y,xi,v5cubic);figure;hold on;subplot(2 ,3, 1);plot(x,y,r*);title(已知数据值);subplot(2, 3 ,2);plot(x,y,r*,xi,yi_nearest,b-);title(最邻近插值);subplot(2,3,3);plot(x,y,r*,xi,yi_linear,b-);title(线性插值);subplot(2,3,4);plot(x,y,r*,xi,yi_spline,b-);t
3、itle(三次样条插值);subplot(2,3,5);plot(x,y,r*,xi,yi_pchip,b-);title(分段三次艾尔米特插值);subplot(2,3,6);plot(x,y,r*,xi,yi_cubic,b-);title(三次多项式插值); (2).二维插值:第一类,二维网格数据插值zi=interp2(x,y,z,xi,yi,method),其中x,y为数据采样点,即为真实所测得的数据,返回值为xi,yi的插值函数值。method与一维插值相同。各个方法所得的插值效果和代码如下:clear;clc;x,y=meshgrid(-3:0.25:3);z=peaks(x,y);xi,yi=meshgrid(-3:0.125:3);z1=interp2(x,y,z,xi,yi,linear);z2=interp2(x,y,z,xi,yi,nearest);z3=interp2(x,y,z,xi,yi,spline);z5=interp2(x,y,z,xi,yi,cubic);subplot(2,2,1);mesh(x,y,z);hold on;mesh(xi,yi,z
4、1+15);axis(-3,3,-3,3,-8,25);title(二维网格双线性插值);subplot(2,2,2);mesh(x,y,z);hold on;mesh(xi,yi,z2+15);axis(-3,3,-3,3,-8,25);title(二维网格最邻近插值);subplot(2,2,3);mesh(x,y,z);hold on;mesh(xi,yi,z3+15);axis(-3,3,-3,3,-8,25);title(二维网格样条插值);subplot(2,2,4);mesh(x,y,z);hold on;mesh(xi,yi,z5+15);axis(-3,3,-3,3,-8,25);title(二维网格双三次插值); 第二类:二维散点数据插值:zi=griddata(x,y,z,xi,yi,method),各个输入值与interp2 的相同,不再赘述。Method为Cubic不能运行,应采用v4方法进行插值。运行代码的效果图如下:clear;clc;rand(seed,0);x=rand(100,1)*4-2;y=rand(100,1)*4-2;z=x.*exp(-x.
《插值和拟合.》由会员我**分享,可在线阅读,更多相关《插值和拟合.》请在金锄头文库上搜索。

高三世界地理专题复习总论4天气与气候汇编

云南大学分析化学第五章 酸碱滴定

南京大学 刘金源教授多元新史观与世界史教学

南大门之不夜城

海南大学 食品分析七 2014

东南大学功放电路和直流电源(第29讲)2014

步步高·2015高三物理总复习(江苏专用)【配套课件】:第4章 曲线运动万有引力与航天 第1课时 曲线运动.

必修2:4.1曲线运动 运动的合成与分解【2015《物理复习方略》一轮复习课件沪科版】.
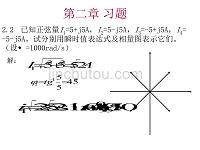
济南大学电工习题答案.

金版学案13-14物理(人教版)选修3-2课件:5.3电感和电容对交变电流的影响.

现代教学媒体.

教案4(火警报警系统).

湖南大学-物理 课程指导八.

语s版六年级下册语文百花园四课件剖析

世纪金榜2018版复习方略物理课件31.

人教新课标二年级语文下册《我不是最弱小的_5》PPT课件.

楼宇自动化 课件 教学PPT 作者 傅海军 第5章.

暨南大学-管理学-第11章-控制.

海南大学 食品分析十二 2014.

北师大八年级数学下册-第2课时-分式的基本性质.
 大学计算机基础知识点总结(30页)
大学计算机基础知识点总结(30页)
2024-04-25 30页
 大学科目《普通地质学》课后思考
大学科目《普通地质学》课后思考
2024-04-25 22页
 《学生手册》考题(含参考答案)
《学生手册》考题(含参考答案)
2024-04-25 7页
 大学科目《采煤概论》复习资料
大学科目《采煤概论》复习资料
2024-04-25 5页
 大一计算机基础知识试题及答案
大一计算机基础知识试题及答案
2024-04-25 8页
 2021年12月大学英语4级CET4听力原文(卷二)
2021年12月大学英语4级CET4听力原文(卷二)
2024-04-23 5页
 2021年12月大学英语6级CET6听力原文(卷一)
2021年12月大学英语6级CET6听力原文(卷一)
2024-04-23 23页
 大学科目《计量经济学》期末试题和答案
大学科目《计量经济学》期末试题和答案
2024-04-23 6页
 2021年12月大学英语4级CET4听力原文(卷一)
2021年12月大学英语4级CET4听力原文(卷一)
2024-04-23 5页
 2021年12月大学英语6级CET6听力原文(卷二)
2021年12月大学英语6级CET6听力原文(卷二)
2024-04-23 10页

