您所在位置：网站首页 > 中学教育 > 试题/考题 > 初中试题/考题2019版数学人教B版选修1-1课件：1.2.1 “且”与“或”

2019版数学人教B版选修1-1课件：1.2.1 “且”与“或”

17页

卖家[上传人]：猪子****y

文档编号：115002225

上传时间：2019-11-12

文档格式：PPTX

文档大小：170.07KB

文档加载中……请稍候！
如果长时间未打开，您也可以点击刷新试试。

下载文档到电脑，查找使用更方便

5 金贝

/ 17 举报版权申诉马上下载

文本预览

下载提示

常见问题

1、1.2.1 “且”与“或” 1.了解“且”与“或”的含义. 2.能判断由“且”与“或”组成的新命题的真假. 【做一做1】用“且”联结命题p,q构成新命题,并判断新命题的真假 : p:16是2的倍数;q:16是8的倍数. 分析:由“且”命题的定义写出新命题:16是2的倍数且是8的倍数. 因命题p,q都是真命题,故新命题是真命题. 解:pq:16是2的倍数且是8的倍数,新命题是真命题. 归纳总结判断“且”命题的真假时,首先判断所给两个命题的真假, 再利用“且”命题的真值表进行判定. 【做一做2】用“或”联结命题p,q构成新命题,并判断新命题的真假 : p:菱形的对角线互相平分;q:菱形的对角线相等. 分析:由“或”命题的定义写出新命题:菱形的对角线相等或互相平分.因命题p是真命题,q是假命题,故新命题是真命题. 解:pq:菱形的对角线相等或互相平分,新命题是真命题. 归纳总结判断“或”命题的真假时,首先判断所给两个命题的真假, 再利用“或”命题的真值表进行判定. 1.如何理解联结词“且”? 剖析:“且”与集合中“交集”的概念有关,与AB=x|xA,且xB 中的“且”意义相同,即“xA

2、”与“xB”这两个条件都要满足.例如, 电子保险门在“钥匙插入”且“密码正确”两个条件都满足时,才会开启,相应的电路就叫与门电路. 2.如何理解联结词“或”? 剖析:“或”与集合中“并集”的概念有关,与AB=x|xA或xB 中的“或”意义相同,它是指“xA”与“xB”中至少有一个是成立的, 既可以是xA,且xB,也可以是xB,且xA,也可以是xA,且xB. 这与生活中“或”的含义不完全相同,例如:“你去图书馆或去游泳馆 ”,两者不可能同时发生,再如,日常生活中,我们认为“苹果是长在树上或长在地里”这句话是不正确的. 名师点拨“且”与“或”只有用来联结两个命题时,才称其为逻辑联结词.如,命题“方程|x|=1的解是x=1或x=-1”中的“或”就不是逻辑联结词. 题型一题型二题型三 “pq”形式的命题及其真假的判定【例1】分别写出由下列各组命题构成的“pq”形式的新命题, 并判断它们的真假: (1)p:30是5的倍数;q:30是8的倍数. (2)p:矩形的对角线互相平分;q:矩形的对角线相等. (3)p:x=1是方程x-1=0的根;q:x=1是方程x+1=0的根. 分析:用逻辑联

3、结词“且”把命题p,q联结起来构成“pq”形式的命题;利用命题“pq”的真值表判断其真假. 题型一题型二题型三反思(1)写“且”命题时,若两个命题有公共的主语,后一个命题可省略主语. (2)判断“且”命题真假的方法和步骤:先判断每一个命题的真假 ;利用真值表判断“且”命题的真假. 解:(1)pq:30是5的倍数且是8的倍数. 由于命题p是真命题,命题q是假命题,故命题pq是假命题. (2)pq:矩形的对角线互相平分且相等. 由于命题p和q都是真命题,故命题pq是真命题. (3)pq:x=1是方程x-1=0的根且是方程x+1=0的根. 由于命题p是真命题,命题q是假命题,故命题pq是假命题. 题型一题型二题型三 “pq”形式的命题及其真假的判定【例2】分别写出由下列各组命题构成的“pq”形式的命题,并判断它们的真假: (1)p:正多边形各边相等;q:正多边形各内角相等. (2)p:线段中垂线上的点到线段两个端点的距离相等;q:角平分线上的点到角的两边的距离不相等. (3)p:正六边形的对角线都相等;q:偶数都是4的倍数. 分析:用逻辑联结词“或”把命题p,q联结起来构成“p

4、q”形式的命题;利用命题“pq”的真值表判断其真假. 题型一题型二题型三解:(1)pq:正多边形各边相等或各内角相等. 由于命题p是真命题,命题q是真命题,故命题pq是真命题. (2)pq:线段中垂线上的点到线段两个端点的距离相等或角平分线上的点到角的两边的距离不相等. 由于命题p是真命题,命题q是假命题,故命题pq是真命题. (3)pq:正六边形的对角线都相等或偶数都是4的倍数. 由于命题p是假命题,命题q是假命题,故命题pq是假命题. 反思(1)写“或”命题时,若两个命题有公共的主语,后一个命题可省略主语. (2)判断“或”命题真假的步骤:判断每一个命题的真假;利用真值表判断“或”命题的真假. 题型一题型二题型三易错题型【例3】 (1)命题“等腰三角形顶角的平分线垂直平分底边”是由“或 ”或“且”构成的新命题吗?若是,指出是哪种形式;若不是,说明理由. (2)命题“不等式x21的解集是x|x1或x-1”的构成形式是 “pq”吗?为什么? (1)错解:不是由“或”或“且”构成的新命题.理由:因为命题中不含有逻辑联结词“或”或“且”. 错因分析:没有注意到该命题是省略联

5、结词“且”的命题. 正解:所给命题可改写为“等腰三角形顶角的平分线垂直且平分底边”,也就是“等腰三角形顶角的平分线垂直底边且等腰三角形顶角的平分线平分底边”,故该命题是由“且”构成的新命题. 构成形式:pq. 题型一题型二题型三 (2)错解:是.因为该命题中含有逻辑联结词“或”. 错因分析:没有注意到“或”联结的不是两个命题. 正解:该命题的构成形式不是“pq”,因为“或”联结的不是两个命题. 1下列命题的构成是“pq”形式的是( ) A.5既是奇数又是质数 B.67 C.不是有理数 D.2是4的约数并且是7的约数答案:B 2下列命题的构成不是“pq”形式的是( ) A.x+1既是x2-1的因式,也是x3+1的因式 B.方程x2=1的一个解是x=1,另一个解是x=-1 C.+2和-2是方程x2-4=0的根 D.函数f(x)=0既是奇函数又是偶函数答案:B 3命题“方程|x|=2的解是x=2”中,使用逻辑联结词的情况是( ) A.使用了逻辑联结词“或” B.使用了逻辑联结词“且” C.使用了逻辑联结词“或”与“且” D.没有使用逻辑联结词解析:命题“方程|x|=2的解是x=2”可以写成“方程|x|=2的解是x=2 或x=-2”,其中的“或”联结的不是两个命题,故没有使用逻辑联结词. 选D. 答案:D 4下列命题中既是“pq”形式的命题,又是真命题的是 ( ) A.15或20是5的倍数 B.1和2是方程x2-3x+2=0的根 C.方程x2+2=0有实数根 D.有一个角大于90的三角形是钝角三角形答案:B 5命题“集合A是集合AB的子集或是集合AB的子集”是命题.(填“真”或“假”) 答案:真

《2019版数学人教B版选修1-1课件：1.2.1 “且”与“或”》由会员猪子****y分享，可在线阅读，更多相关《2019版数学人教B版选修1-1课件：1.2.1 “且”与“或”》请在金锄头文库上搜索。

点击阅读更多内容

TA的资源

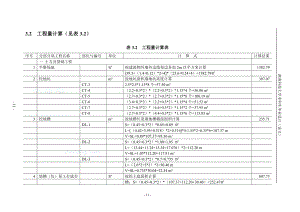
第三章工程量计算_secret-经典通用工程施工资料

地下室混凝土-经典通用工程施工资料

毕业设计任务书(1)-经典通用工程施工资料

V 南湖变电站工程施工组织设计方案-经典通用工程施工资料

13天桥设计-经典通用工程施工资料

GANGJIN-经典通用工程施工资料

12基础设计(1)-经典通用工程施工资料

高中生自查报告范文-经典通用

0003 土方工程施工方案-经典通用工程施工资料

高职机械类专业教育校企深度合作的路径与对策-教育文档-经典通用-经典通用

A3演示文稿设计与制作—初中数学对顶角及其性质【微能力认证获奖作品】

第三章基础数据_secret-经典通用工程施工资料

地下室模板-经典通用工程施工资料

第七章主要施工方法及技术措施-经典通用工程施工资料

毕业设计任务书(施工)_secret-经典通用工程施工资料

12章工期保证措施及应变措施-经典通用工程施工资料

03目录_secret-经典通用工程施工资料

v变电站加固工程施工组织设计方案-经典通用工程施工资料

高中生寒假社区社会实践报告-1-经典通用

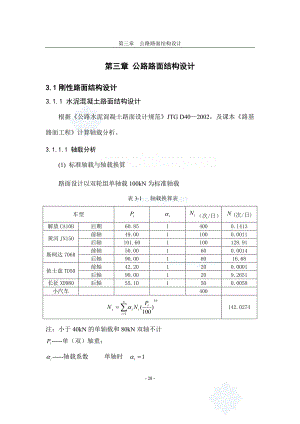
第三部分公路路面结构设计_secret-经典通用工程施工资料

点击查看更多

新上传的PPT文档

公司车辆维修定点合同场地硬化业务合作协议书(独家合作) 中华魂演讲稿模板集合5篇六年级数学毕业模拟检测试卷16 新闻报道培训心得（可编辑）大学生专业实习报告10篇孕产妇备物品清单从青啤的发展战略调整看中国啤酒工业未来发展方向（阅）篝火晚会结束语大全 2023年季运动会广播稿集锦15篇（可编辑）经理辞职报告例文石方爆破技术业务产品审批、许可证、产能、质量情况实用的开学典礼主持词3篇